La Danza della Terra

La Precessione degli Equinozi

Analisi Dinamica e Modelli Scientifici
Questo documento esplicativo accompagna la simulazione numerica del moto secolare terrestre, regolata su un'inclinazione di 23.4° e in modalità Sincronia Globale. Il modello integra le leggi di Keplero con la variazione secolare dell'asse, scoperta da Ipparco di Nicea e spiegata fisicamente da Isaac Newton.

1. Perché abbiamo le stagioni?

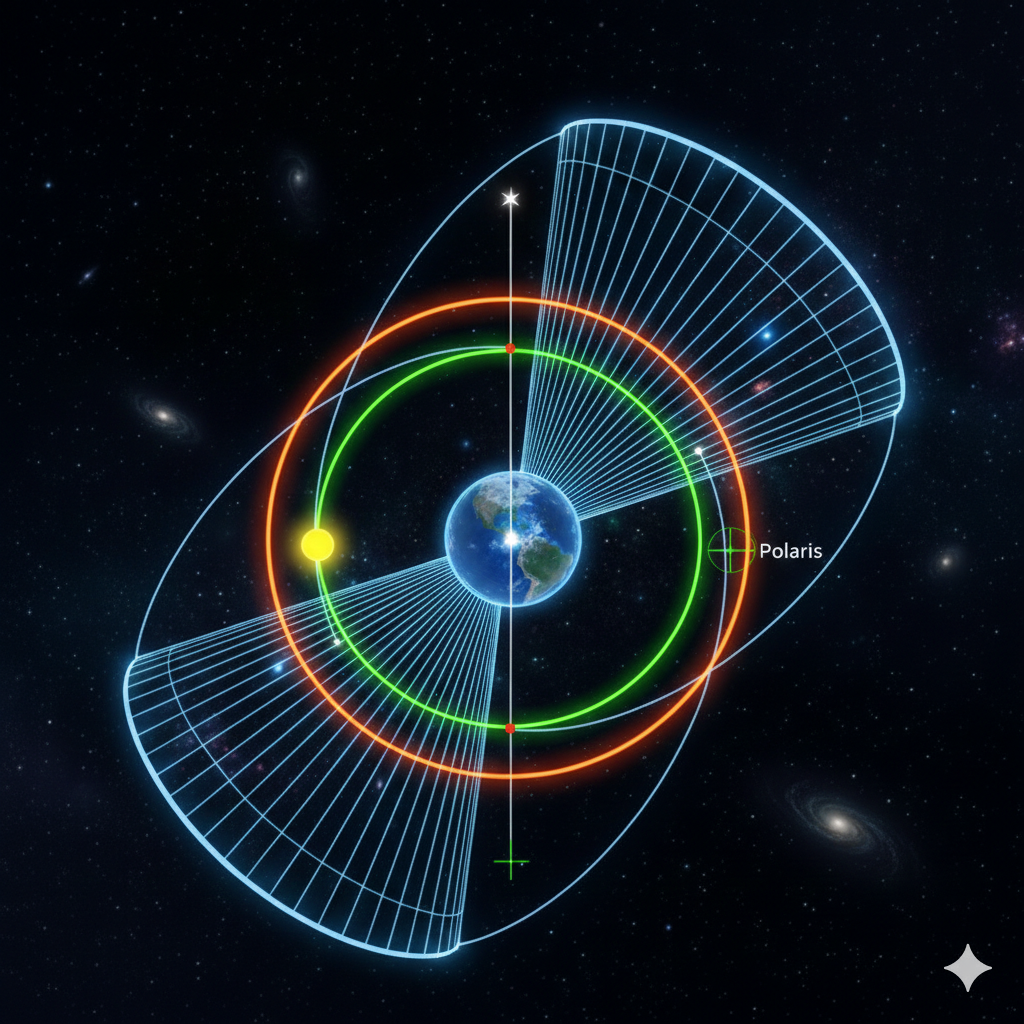
Il "giroscopio" terrestre: l'asse ruota disegnando un doppio cono.

Le stagioni non dipendono dalla distanza dal Sole, ma dal fatto che la Terra percorre l'orbita attorno al Sole con l'asse di rotazione inclinato di circa 23,5°. Questa inclinazione fa sì che la luce solare colpisca i due emisferi in modo diverso durante l'anno.

Questa geometria fissa sulla Terra dei confini immaginari molto importanti per il clima:

Circoli Polari: Dove il sole può non tramontare mai (a circa 66,5° di latitudine).
Tropici: Dove il sole arriva esattamente a picco sopra di noi (a circa 23,5° di latitudine).

2. Il "Grande Anno" (Ciclo di 26.000 anni)

L'asse della Terra si comporta come una trottola che sta per fermarsi: la punta disegna un cerchio nel cielo molto lentamente, completando un giro ogni 25.772 anni. Gli antichi chiamavano questo periodo Anno Platonico.

Curiosità: Platone pensava che alla fine di questo enorme ciclo, tutte le stelle e i pianeti sarebbero tornati al punto di partenza, dando inizio a una nuova era.

3. La geometria del cerchio celeste

Se guardassimo l'asse terrestre proiettato nel cielo, vedremmo che descrive un cerchio perfetto. Matematicamente, la posizione di questa "punta" nello spazio è calcolata così:

X_p = R \sin(\epsilon) \cos(\omega_p t)$$ $$Y_p = R \sin(\epsilon) \sin(\omega_p t)$$ $$Z_p = R \cos(\epsilon)

4. Come la Terra si muove nello spazio

Mentre l'asse ruota, la Terra continua a girare attorno al Sole seguendo un percorso a forma di ellisse (un cerchio leggermente schiacciato), regolato da questa formula:

r(\theta) = \frac{a(1 - e^2)}{1 + e \cos \theta}

5. Cambiamenti nel tempo: Ieri, Oggi e Domani

A causa di questo movimento, la stella che indica il Nord e le date delle stagioni cambiano nei millenni:

Cosa cambia	13.000 Anni Fa	Oggi	Tra 13.000 Anni
Stella del Nord	Vega	Stella Polare	Vega
Inizio Primavera	Settembre	21 Marzo	Settembre

6. Perché l'Equinozio arriva "in anticipo"?

L'equinozio avviene quando l'asse terrestre si trova in una posizione specifica rispetto al Sole. Ma poiché l'asse ruota lentamente come una trottola, esso cambia orientamento andando incontro alla Terra mentre lei sta ancora percorrendo la sua orbita.

Il punto d'incontro: Ogni anno la Terra "incrocia" l'equinozio circa 20 minuti prima di aver completato un giro intero rispetto alle stelle fisse.
Moto Retrogrado: Immagina di correre in un cerchio verso un traguardo che si sposta verso di te: lo raggiungerai ogni volta un po' prima. Rispetto alle stelle sullo sfondo, il Sole sembrerà "scivolare all'indietro" lungo lo zodiaco.

7. Calcolo delle zone climatiche

L'inclinazione dell'asse ($\epsilon$) definisce matematicamente dove si trovano i tropici e i circoli polari sulla mappa geografica:

\text{Tropici} = \pm \epsilon$$ $$\text{Circoli Polari} = \pm(90^\circ - \epsilon)

8. Guida all'uso del simulatore

Nella simulazione puoi vedere il movimento in azione. Ecco alcuni dettagli per capire cosa succede nel simulatore:

Cos'è un Anno Orbitale? In astronomia, è il tempo impiegato da un pianeta per compiere un giro completo di $360^\circ$ attorno alla sua stella. Per la Terra, corrisponde a circa 365,25 giorni.
Perché proprio "27" anni? È un parametro di compressione temporale per rendere visibile un fenomeno altrimenti troppo lento.
- La realtà: L'asse completa un giro in 25.772 anni.
- La simulazione: Il modello accelera la precessione. Ogni rivoluzione completa attorno al Sole, l'asse si sposta di ben $13,3^\circ$.
- Il Ciclo Completo: Poiché $13,3^\circ \times 27 \approx 360^\circ$, in soli 27 anni orbitali l'asse completa il suo intero cerchio.
In sintesi: Dire "27 anni orbitali" significa che nel simulatore il tempo è accelerato di circa 1.000 volte rispetto alla realtà.
Sincronia Globale: Se attivata, collega perfettamente il movimento della Terra attorno al Sole con la rotazione del suo asse.
Analisi tecnica: Ogni anno che passa nel simulatore, l'asse si sposta di un angolo visibile pari a: $$\Delta\phi = \frac{360^\circ}{27} \approx 13.3^\circ$$

💡 Il Calendario e il Clima

Sapevi che l'anno solare (quello delle stagioni) è più corto di circa 20 minuti rispetto al tempo che la Terra impiega per fare un giro completo attorno al Sole? Questo piccolo scarto, accumulato nei millenni, influenza i grandi cambiamenti del clima terrestre.